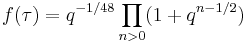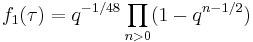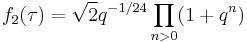Weber modular function

In mathematics, the Weber modular functions are a family of three modular functions f, f₁, and f₂, studied by Heinrich Martin Weber.

Definition

The complex number q is given by e^2πiτ where τ is an element of the upper half-plane.

$\displaystyle f(\tau) = q^{-1/48}\prod_{n>0}(1%2Bq^{n-1/2})$

$\displaystyle f_1(\tau) = q^{-1/48}\prod_{n>0}(1-q^{n-1/2})$

$\displaystyle f_2(\tau) = \sqrt2q^{-1/24}\prod_{n>0}(1%2Bq^{n})$

The transformation τ → –1/τ fixes f and exchanges f₁ and f₂. So the 3-dimensional complex vector space with basis f, f₁ and f₂ is acted on by the group SL₂(Z).

References

Weber, Heinrich Martin (1981) [1898] (in German), Lehrbuch der Algebra, 3 (3rd ed.), New York: AMS Chelsea Publishing, ISBN 978-0-8218-2971-4, http://www.archive.org/details/lehrbuchderalgeb03webeuoft
Yui, Noriko; Zagier, Don (1997), "On the singular values of Weber modular functions", Mathematics of Computation 66: 1645–1662, doi:10.1090/S0025-5718-97-00854-5, MR 1415803